Last year, LeanBI successfully implemented a Deep Learning project for the engineering company Amberg AG, in which the efficiency of tunnel maintenance was increased by 60%. The AI component developed by LeanBI and based on image segmentation using deep learning has meanwhile been integrated into the maintenance software of Amberg.

The manual evaluation of images or laser scans from tunnels is extremely time-consuming and is often performed by engineers. Luckily, a big part of the process can be automated using deep learning for object detection and segmentation. A deep network detects damages such as cracks or wet areas, but also other objects of interest like pipes or electrical boxes in the tunnel. The network is not only able to detect objects, but also identify the exact pixels associated to them on the image. This is of tremendous help to the engineers, as they originally had to draw by hand polygons around damaged areas, or lines annotating cracks. Now they only need to follow the software’s proposal, and confirm the automatically detected damages, or edit the automatic annotation before confirming.

One of the challenges that most deep-learning projects face, is the need for a large amount of training images, that must be labelled manually. By choosing the right family of deep networks and customizing it to be able to learn with less data, we were able to obtain very good accuracy with only a few hundreds of meters of annotated images. Another factor that played a crucial role to our success was the efficient use of the labelled data. When the labelling process is expensive (costly or time consuming), we can use what is called data augmentation, to artificially increase the amount of labelled data we can use for training and achieve much better accuracy.

A further benefit of our solution is that it automatically quantifies uncertainty. This means, that when it identifies an object, it also gives a probability of how “surely” this object is in the identified class. Is the object wet with a 99% certainty, or only with 60%? This information is important to prioritize and save time in the final tunnel evaluation.

Alzbeta Prokopova, Application and Support Engineer at Amberg AG was interviewed by Tunnelling Journal about this project. You can find the whole interview in the Feb/Mar 2020 issue  on page 11.

LeanBI has helped Amberg to implement part of the solution in the cloud, which has massively reduced the analytical costs. This is not only a technical challenge, but also an economic one, as large government institutions and large engineering companies must be convinced of the security and reliability of data storage in the cloud.

Amberg has also solved the problem that no Internet connection can be established in the tunnels. They therefore developed an offline version of the software that can be synchronized with the Internet as soon as network connection is available.

Automating damage detection with Deep Learning not only increases productivity, but also improves the quality and consistency of the detection. By automatizing the process, it is also easier to track temporal changes in tunnels, by running the same deep network on images of the same tunnel captured in different periods.

With the maintenance solution from Amberg Engineering and with the support of LeanBI, tunnel inspections can therefore be carried out as required and not at a fixed rigid schedule as was previously the case.

Prescriptive Analytics is a further step in applied data analysis. It is also an important basis for improving the results of predictive analytics.

In the field of Business Intelligence, the “Analytics maturity model” from Gartner is generally known. We illustrate this in a somewhat extended form in Figure 1.

Figure 1: The maturity model of data analytics according to LeanBI based on the Analytics maturity model according to Gartner

Along the stages, the complexity of data analysis increases from bottom to top. The original area of Business Intelligence covers reporting and data analysis (in LeanBI with OLAP,Online Analytical Processing, using multidimensional cubes). The upper area of Data Science can be divided into predictive and prescriptive analytics. Most of today’s data science use cases deal with predictive analytics and leave prescriptive analytics out. Thus, most of today’s models such as Deep Learning can be used to detect patterns in order to predict, for example, the damage of a machine component, as LeanBI does with LeanPredict. With predictive analytics, however, it is less easy to draw conclusions about the causes of the damage, the more difficult it is the wider the models are. Therefore, in this blog we want to deal with the topic of prescriptive analytics, especially the modelling of causes.

Quantifying the effect of a factor

Trying to find the cause that can lead to a change in a product we want to optimize can be tackled by different techniques depending on context. In marketing, for example, we want to answer questions like “does the position of the button change the click rate of the user?”. In this context, we have the freedom to change the parameters (the position of the button) and use A/B testing to measure the actual effect of the change between users clicking the button in the old position and users clicking the button in the new position.

On the other side, in predictive maintenance, we want to answer questions like “does the change of the rotation speed that I observed last month lead to earlier breaking of the machine?”. In this case, if we assume that the change of speed happened without our intervention (like an anomaly) and we do not control it directly, we can only measure its effect based on observations. We must analyze the machines that broke or not, and which of them had an unexpected change in the rotation speed or not. In this type of problems, where we do not have control over the parameters in question, and we can thus not set up experiments, but only observe results a posteriori, we need to use the mathematical models of the field of causal inference.

Causal inference and causality versus correlation

There are different approaches in the field of causal inference. One of the most important representatives in the field is Judea Pearl, who has been honoured with many awards, including the well-known Turing Award in 2011. He is the pioneer of Bayesian networks, causal models about which we want to write today.

Predictive analytics has its pitfalls when we fail to take influencing factors into account sufficiently in our models. We bring a medical example from Judea Pearl, because it is very clear to all of us: If we apply the influence of sporting activities to the cholesterol level, we get a dependence according to Figure 2.

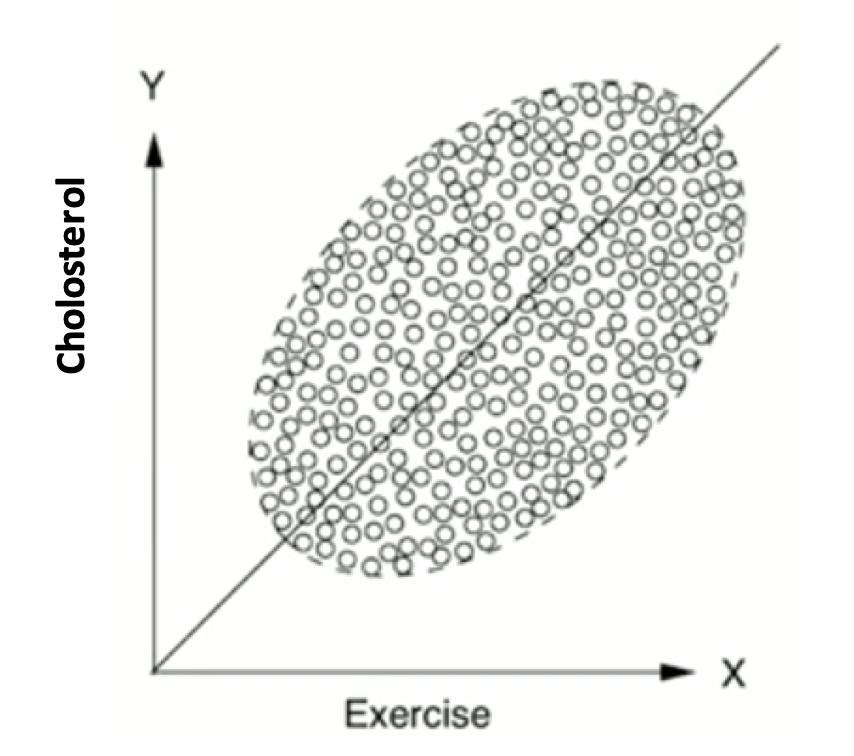
Figure 2: Dependence of cholesterol levels on sporting activities according to [1].

We interpret that more sport leads to higher cholesterol levels because we see a high correlation between the two variables. Actually, we don’t expect that. So what’s wrong? – We’ve overlooked an important factor, which is age. If we take this parameter into account additionally, we suddenly interpret the same amount of points quite differently, by grouping people by age before analyzing each group separately. As expected, there is now a negative correlation between cholesterol and amount of sports for each group. Why was this not obvious before? Because for this data, older people not only have higher cholesterol, but also fight against it by doing more exercise. Age causes both parameters to increase, so they seem highly correlated if we do not take age into account. When we “control for age”, however, we understand that it is the cause of higher exercise and of higher cholesterol at the same time. But most importantly, exercise is also a cause for lower chelosterol (see Figure 3).

Figure 3: Inclusion of the influence of age on the cholesterol level according to [1].

Wrong interpretations like the one of Figure 2 can happen in Data Science, because wrong parameters are included in the models or because the importance and relationship between the parameters are misidentified. This can then have more or less serious consequences. At the very least, such misinterpretations from inadequate models are accompanied by a loss of confidence in the data science capabilities.

Therefore, we see that research into the causes and relationships of different effects is important in order to have more meaningful modelling. With causal research, the correlations of analytical models become causalities.

Causal inference in the industry

How do we do this in our field of industrial data analysis? In industrial data analysis, we detect an approaching damage due to a deviation of the measured data from normality (like an anomaly). We call these measurement data “effects”. Let’s take temperature as an example. If a temperature increases at the location of a surface, it may be possible to predict an approaching damage. But how certain can we be?

Let us look at the following generic graph:

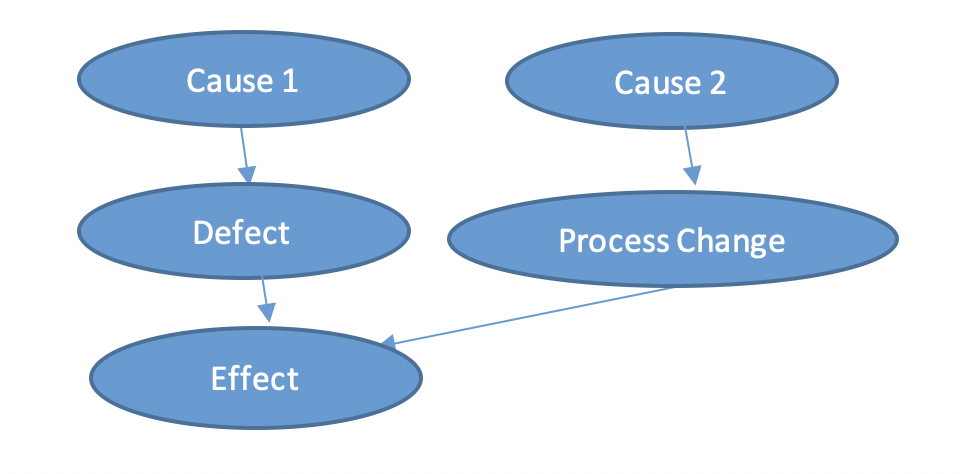
Figure 4: Causes – Effect – Graphical model of a machine damage

A measured (“observed”) effect can have several reasons and each reason has one or more causes. However, if we have not paid enough attention to the causes and interrelationships of the effects, there is a risk that we will produce false alarms. This is because an increase in temperature can have several reasons, for example a process change or damage to a component. So we have to find out the causalities, which requires specialists in the relevant fields. For LeanBI, this means holding workshops with the specialists on site, be the engineers or production operators.

So when we have a better understanding of the cause-effect chains, we can define probabilities of which effects will occur under which conditions. What is the procedure? We form causal networks, so-called graphical models. An important representative of causal models is the “Bayesian Network”. Figure 5 again shows a plausible example from medicine. We form probabilities for each effect and write them in tables.

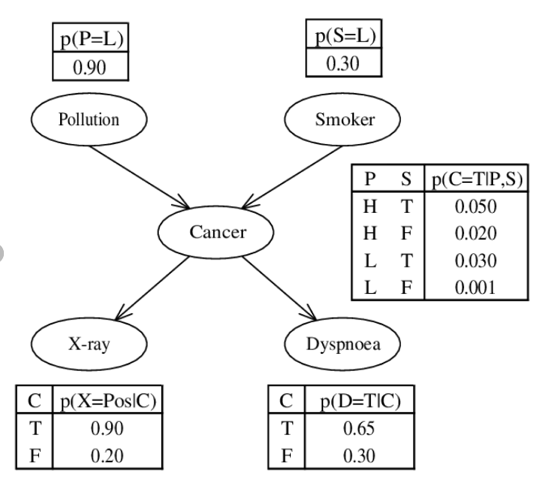
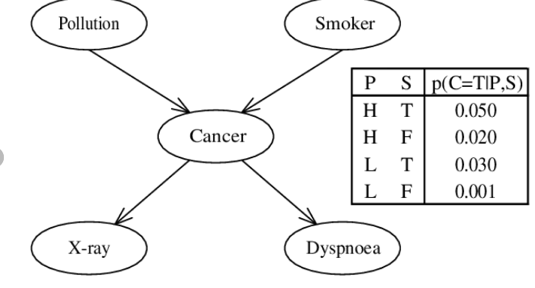
Figure 5: Example of a simple “Bayesian Network” graph: Connection of lung cancer according to [2]

Take the table in the middle, for example: If we have P (Pollution) = H (High) and S (Smoker) = T (True), the probability of getting cancer is 0.05, as a non-smoker S (Smoker) = F (False) in the same environment is only 0.02. The results of different effects/measurement methods such as X-Ray or dyspnoea (respiratory difficulty) indicate with certain probabilities that cancer is present. It is therefore necessary to determine the probabilities with studies, experiments or with the help of the field experts.

It can be very complex to evaluate correct cause-effect mechanisms, and the interpretation is difficult. For example, events do not have to occur simultaneously and can even change over time. Therefore, a central point is to ask the right questions about the network (Judea Pearl calls this “Do Operator”). Questions here are also counter-questions: What would have changed if event B had never occured? These are called “counterfactuals”. “What if it’s not cancer, as shown by the x-ray?” With such questions we enrich the network and improve it.

The exciting thing is that the graphical models can be transferred 1:1 into mathematical models. An important term for this is conditional probability. We determine the probability of an event A under the condition that event B applies. This is written as P(A I B) or PB (A). In the Bayesian network this is how the nodes are described. And with this the mathematical model of the whole graph can be built.

The Bayesian Network models mathematically represent a cause-and-effect reality that we have recognized. It is a reality reduced to influences and areas of interest to us, and always associated with uncertainties. Within such networks we can explore reality by applying and varying the mathematical models. In this way, we expand our knowledge space in terms of modelling. This is a great advantage, because we can hardly experiment with people to better understand the causes of cancer (like marketing experts do with A/B testing). Exactly the same in an industrial environment. The data situation is limited and test data is expensive or not available at all. The models help us to better understand the machines and their damage out of their observed behaviour.

Were expert systems not already solving the problem?

Given that we use input from field experts to create causal models, it makes sense to compare them to old style expert systems. But there is a fundamental difference between the two approaches. In expert systems, the know-how of the field experts was hard coded in the “inference engine”, in the form of logical rules, not as probability distributions. The experts were coding clearly understood failure mechanisms, that of course is very restrictive and not possible for many use cases. At that point, there was no machine learning involved, so this type of systems did not go that far.

In causal inference, on the other hand, the experts give a range of possible mechanisms that could lead to a failure, to create one or more causal graphs. Then it is up to the data to explain / quantify which of the cases is more plausible, while the experts can in a next iteration refine the models based on that. Once the models are fixed, we can use them to perform not only diagnostic analytics, but also predictive and prescriptive.

Looking into the future

Finding the cause of a failure (“why did it happen”) per se falls mostly in the category of diagnostic analytics. However, once we have a causal model fit to our data, we can use it as a soft form of the process’s digital twin. The model is a powerful tool that we can use for predictive, but also prescriptive analytics.

Modern machine learning, with deep learning as its flagship have tackled many problems that were unimaginable 10 years ago. However, today’s new need is more and more to have interpretable, or explainable models, and deep learning by itself is not enough. Probabilistic machine learning and modelling can fill this gap, se we already see a new trend of deep learning combined with probabilistic modelling being shaped. It is not a coincidence that the most used deep learning library today, Tensorflow, added very recently a “probability” module incorporating very important inference tools. The possibilities are endless.

Prescriptive Analytics is a further step in applied data analysis. It is also an important basis for improving the results of predictive analytics. LeanBI, looking into the future, is investing in this direction. In the future, LeanBI will increasingly combine both stages directly with each other. Thus, the result of a Bayesian Network can be the input for Deep Learning. A node of a Bayesian Network can be a Deep Learning model. Or the prediction of a Deep Learning Model flows into a Bayesian Network to better identify the cause of a problem.

Literature:

[1] Keynote: Judea Pearl – The New Science of Cause and Effect, PyData LA 2018: https://www.youtube.com/watch?v=ZaPV1OSEpHw&t=3299s

[2]: Particle swarm and bayesian networks applied to attribute selection for protein functional classification, 2007